Three General Patterns for Adaptive Ensembles
The adaptive ensemble (implemented in the library “AdaEnsemble”) consist in a multi armed bandit algorithm that chooses between different machine learning models, and passes the data passed to the ensemble down to the selected machine learning model. The output of the selected model, given the data, is the output of the ensemble. Here are three patterns by which adaptive ensembles might be applied. Importantly, the member models of each ensemble can be from any family of machine learning models, if they produce an output that can be used to calculate a reward. This straightforwardly includes all supervised learning algorithms and reinforcement learning.
A Brief Note On Charts
In the charts that follow, each line represents a model that can be chosen by the ensemble, and the line thickness represents whether a model is more or less likely to be picked by the ensemble. They have been created purely for illustrative purposes and do not show the actual mechanics of an ensemble, which depend on many factors and make consise visualisation pretty difficult.
1. Online model selection on static models: the adaptive ensemble picks the best model of two or more machine learning models. The models do not adapt to new data, but the ensemble reacts to feedback and applies the model that is better at a given time.
In the example, the generating process consists in either returning a constant value or a sine transformation of that value, but always one or the other for prolonged stretches of time. The two lines represent two models that were trained on prior data. These models do not change with incoming data, but the adaptive ensemble learns to pick the better model given recent feedback. The likelihood of a model being picked by the ensemble is represented by the thickness of the line.
An example with convolutional image classifiers in the case of pipeline underspecification can be found in the post on mitigating pipeline underspecification.
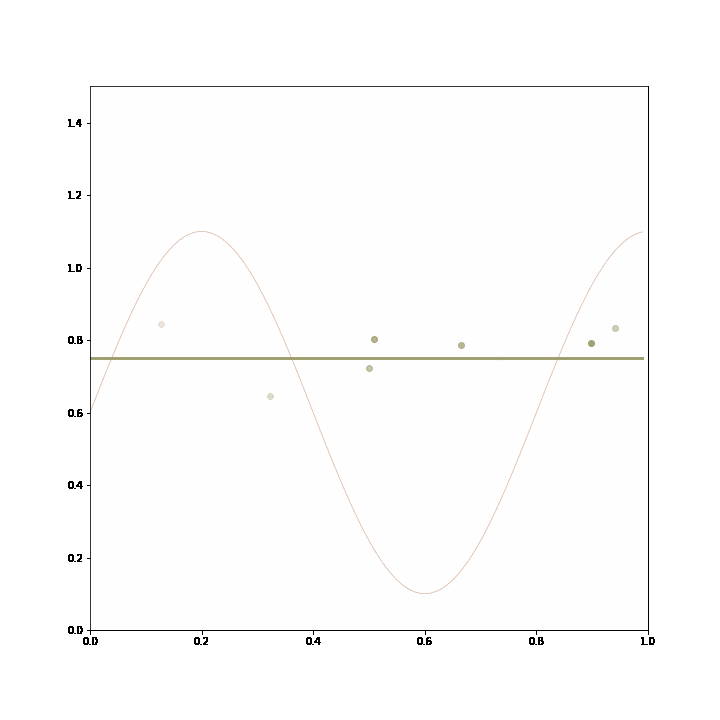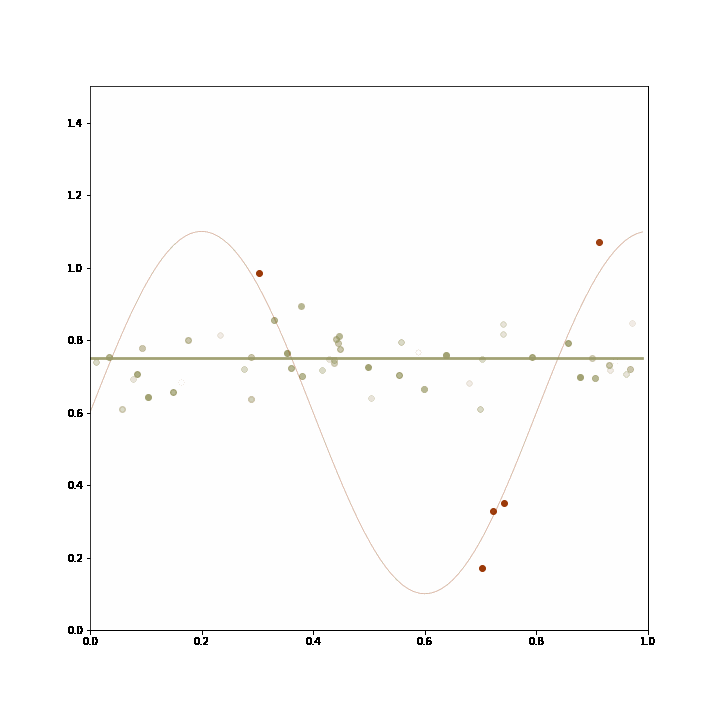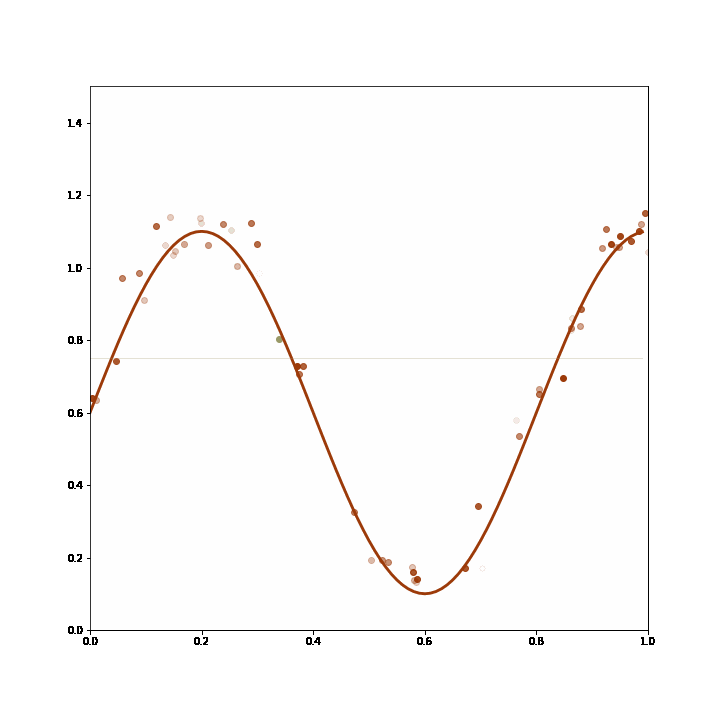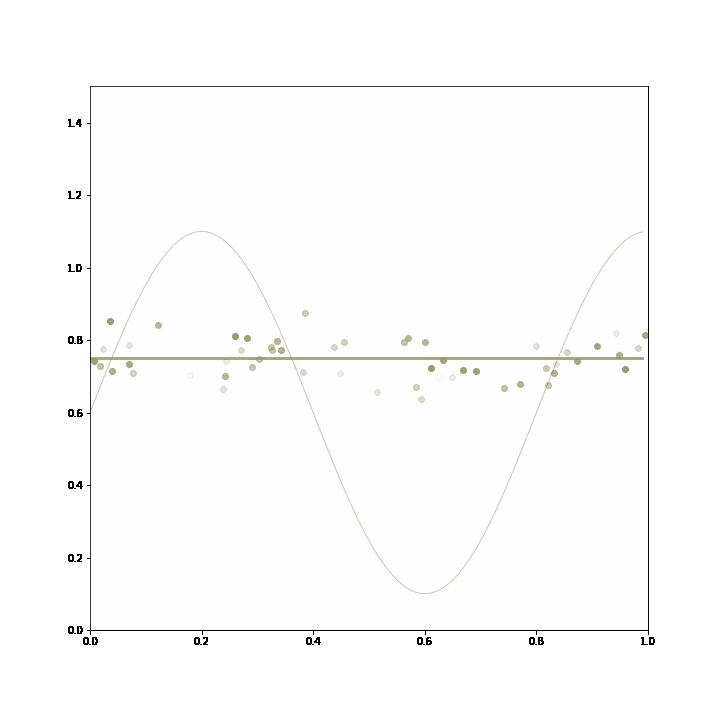
The ensemble starts out picking the linear model, then changes to pick the sinusoidal model after the data changes so that it fits better, and then reverts to the linear model as the data changes yet again.
2. Incremental learning with insurance: the adaptive model contains one or more incremental machine learning models and one or more static models. The incremental learners can adapt to new data, but in case they diverge or perform worse than the alternative static model for another reason, the ensemble can choose to go back to the static model. In this way, incremental learning might be introduced to a use case with the knowledge that in the worst case the ensemble reverts back to the established static model.
At first, the static model conforms well to new data, and is picked most frequently by the ensemble (represented by the thicker line). Then, the data generating process changes and the incremental learning proves superiour, and thereby is selected more frequently by the ensemble. Towards the end, it changes again and the static model performs better again, and the ensemble switches back to using the static model.
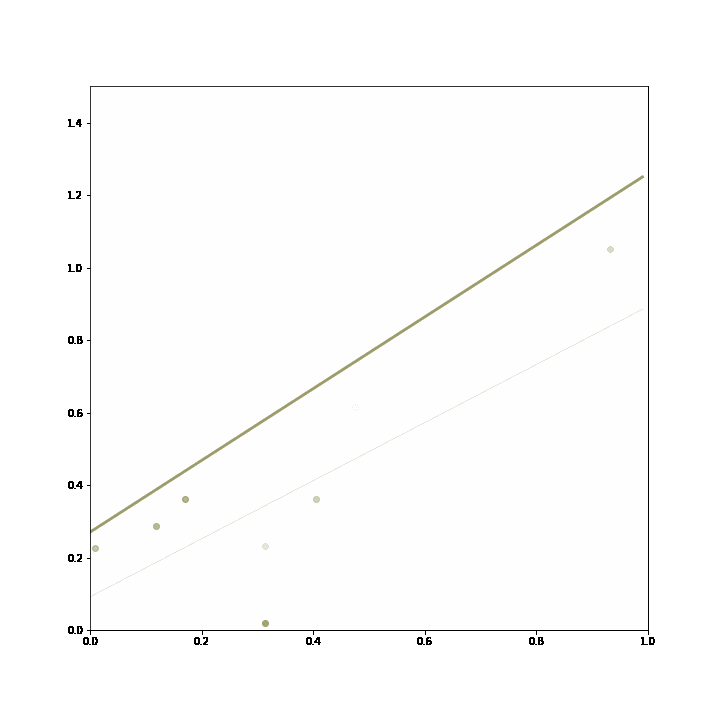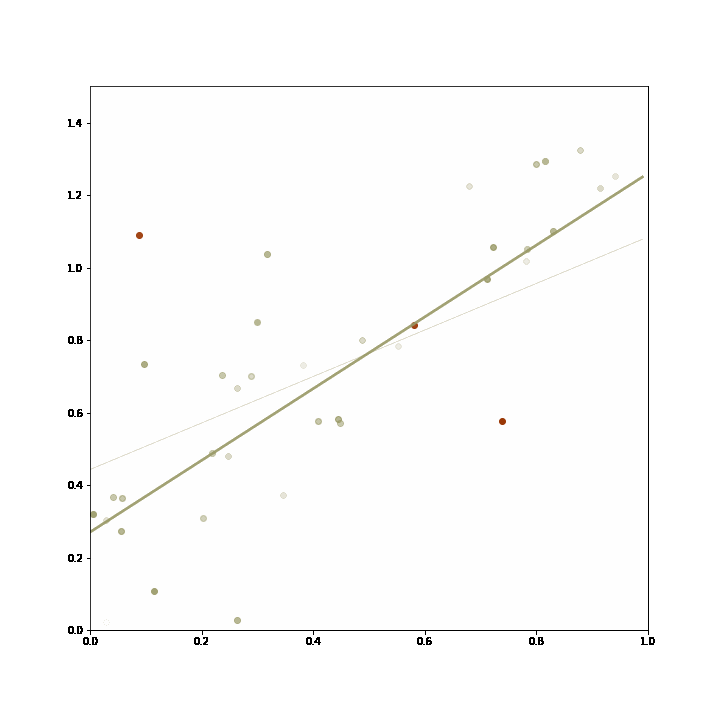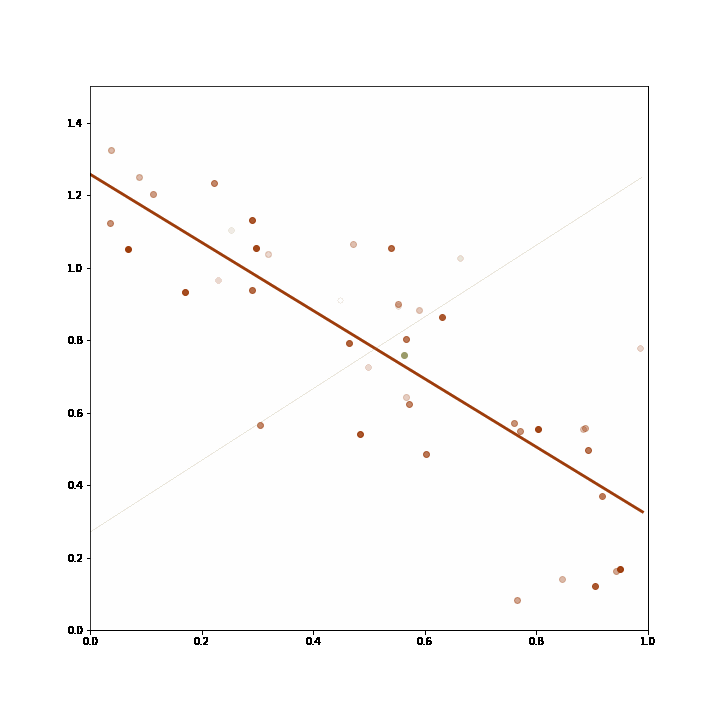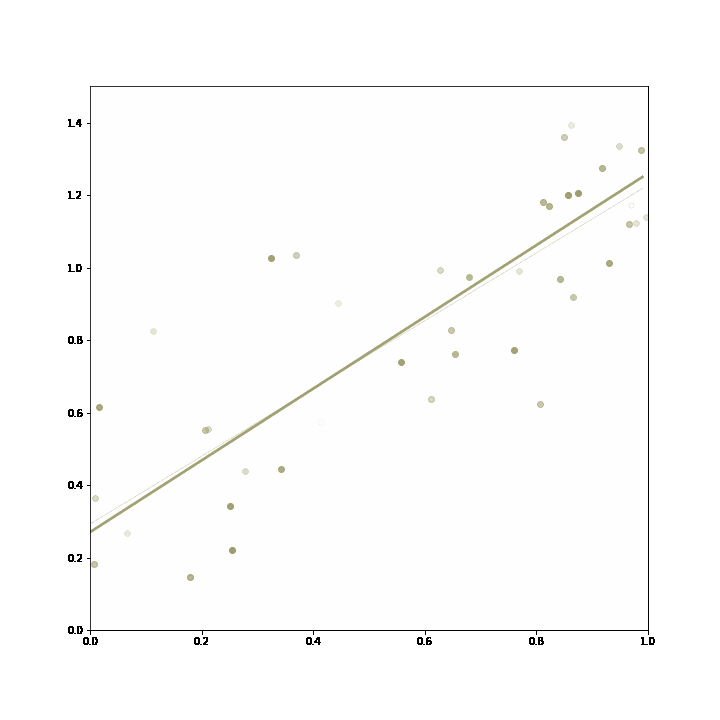
The ensemble starts out relying mainly on the static model trained in advance. As the data changes, the incremental linear regression starts to fit the data better, and it is chosen more frequently by the ensemble. Then, the data reverts to its previous behaviour and the ensemble returns to the static model.
3. Online hyperparameter tuning: an incremental learning algorithm might take have multiple hyperparameters that need to be set at the outset. Algorithms with different settings can just be bundled into an adaptive ensemble, which will learn to apply the model with the best available hyperparameters. In this example, the hyperparameter is the number of previous data points that are used for regression, and the the regression based on a longer horizon proves superiour, and is selected by the ensemble.
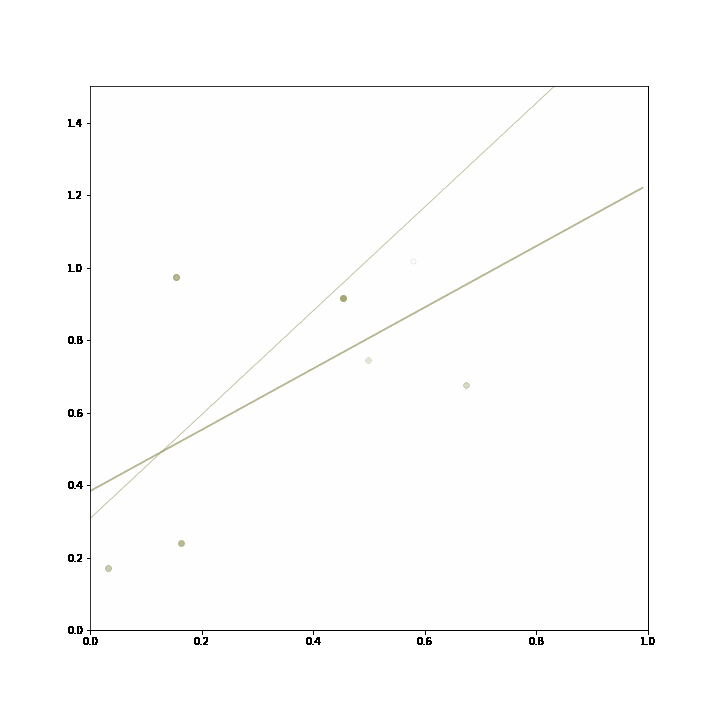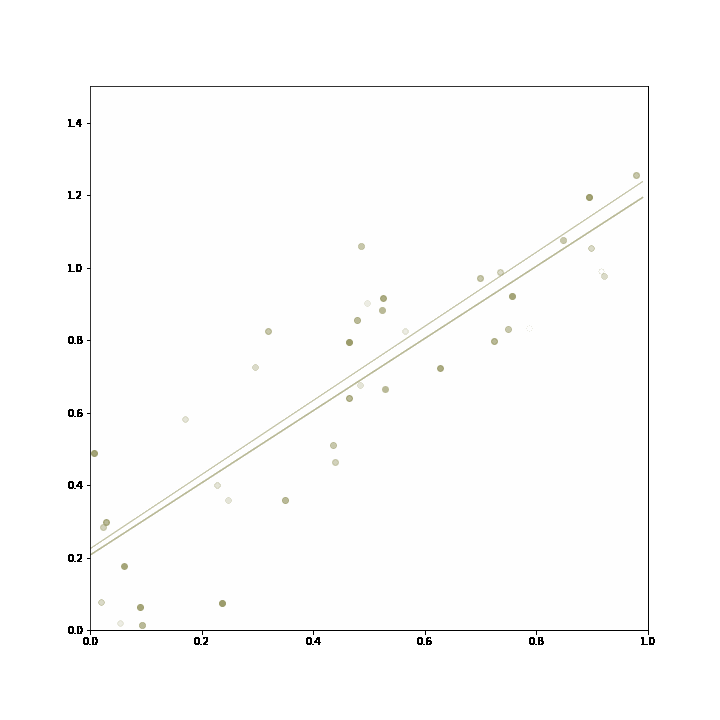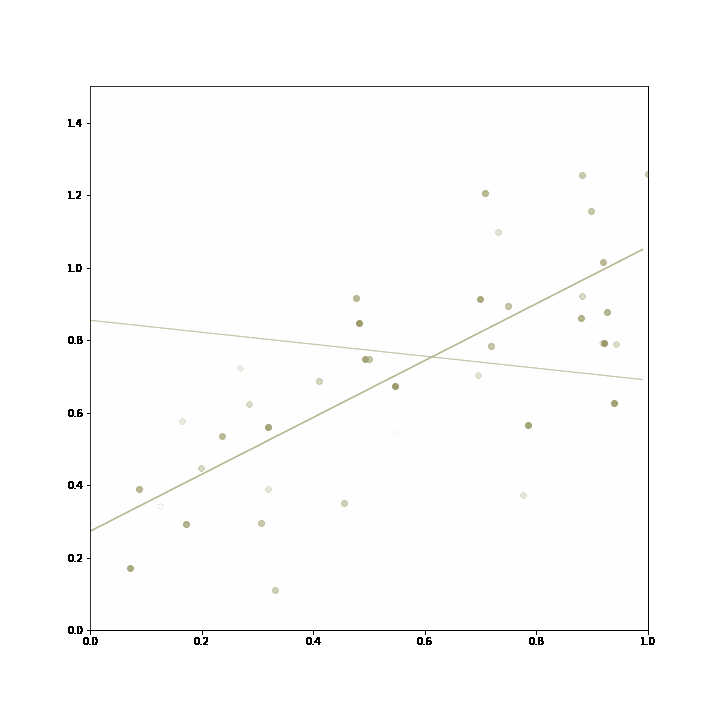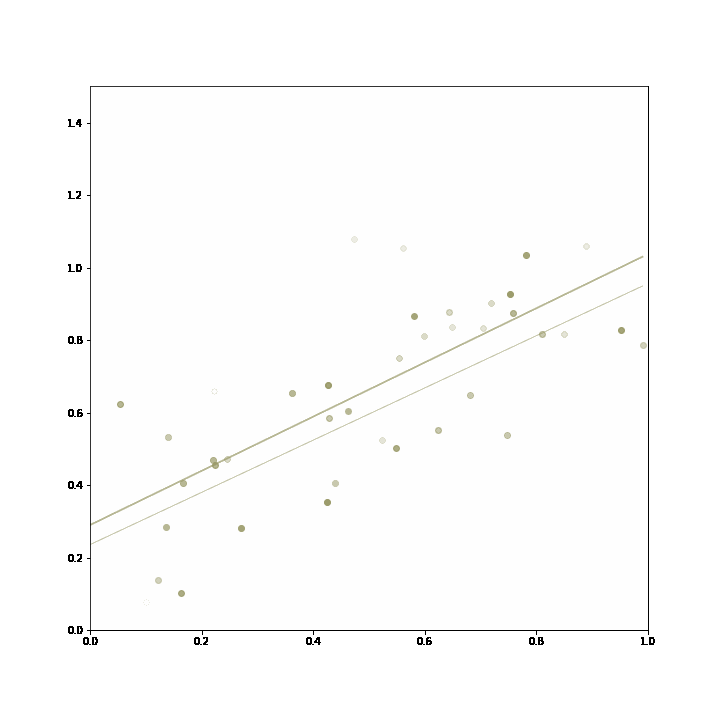
The ensemble starts out choosing both incremental linear regression equally often, and then converges on the model with the longer training horizon, as it proves more accurate in its predictions.
A technical introduction to the AdaEnsemble library can be found here.